I’ve been reading Concurrency Control and Recovery in Database Systems as part of Phil Eaton’s software internals book club. I’m currently working my way through the third chapter on two phase locking (2PL). I’ve had some light exposure to transaction serializability and 2PL in the past. I even wrote a toy transaction scheduler complete with strict 2PL and deadlock detection using a wait-die algorithm for victim selection. However I had a lot of gaps and was missing a larger view of serializability theory.
A serializable history (or schedule) is one that is equivalent to some serial execution of transactions. For example, given two transactions T1 and T2 it would have two possible serial histories T1->T2 or T2->T1. A concrete example might look like this:
T1->T2
T1: BEGIN
T1: R(A)
T1: W(A)
T1: W(B)
T1: COMMIT
T2: BEGIN
T2: W(A)
T2: R(B)
T2: COMMIT
T2->T1
T2: BEGIN
T2: W(A)
T2: R(B)
T2: COMMIT
T1: BEGIN
T1: R(A)
T1: W(A)
T1: W(B)
T1: COMMIT
Serializable histories are important because they ensures that concurrent transactions produce a correct and consistent result, as if they were executed one after another. An example of a serializable history would be:
W2[A],R1[A],R2[B],C2,W1[A],W1[B],C1
Translated into a timeline it looks like:
T2: BEGIN
T2: W(A)
T1: BEGIN
T1: R(A)
T2: R(B)
T2: COMMIT
T1: W(A)
T1: W(B)
T1: COMMIT
This is equivalent to a serial order T2->T1. However, you might notice that this example contains a dirty-read. Transaction T1 reads the write of a another transaction, T2, before it committed it’s results. If T2 had aborted instead of committed then things would be in a incorrect state. What would have to happen is that T1 would need to be made dependent on T2 and abort along with it. This is known as a cascading abort, and they are challenging to implement and generally avoided in practice. The full landscape of serializability is actually quite large.

Our example is both recoverable and conflict serializable, but it doesn’t avoid cascading aborts, which is a desirable property to have. One way to avoid cascading aborts is if the history is strict. A strict history is one such that whenever a conflicting write operation occurs (write-read or write-write) then the transaction that did the first write needs to commit or abort before the following read/write operation can happen.
Read-write conflicts are also conflicting, but in the case of strict, conflict serializable histories, they are permitted since aborting the reading transaction doesn’t affect correctness.
One way to achieve strict, conflict serializable schedules, is by using 2PL. I won’t get into 2PL in this post, but just know that it consists of two phases:
- The growing phase, during which a transaction can acquire locks.
- The shrinking phase, during which it can only release them.
Once a transaction releases any lock it can’t acquire any new ones.
In chapter 2 of the book, Bernstein succinctly describes the theorem of conflict serializability, “A history H is serializable iff SG(H) is acyclic.”
Here, SG(H) is the serializability graph of a history. You can build a serializability graph quite simply by looking at the conflicting operation (read-write, write-read, or write-write). If conflicting operation between T1 and T2 occur and the T1 operation comes first then you draw an edge from T1->T2. We can use our example serializble history from earlier (W2[A],R1[A],R2[B],C2,W1[A],W1[B],C1) to showcase this.
Because W2[A] conflicts with R1[A] and T2's operation comes first we would draw the edge from T2->T1. R2[B] also conflict with W1[B] and again T2's operation comes first so the edge from T2->T1 still holds and the graph is acyclic and therefore it’s conflict serializable.

An example of a non serializable schedule with our example transactions is the following:
R1[A],W1[A],W2[A],R2[B],W1[B],W2[B],C1,C2
W1[A] proceeds and conflicts with W2[A] so we draw an edge from T1->T2. R2[B] proceeds and conflicts with W1[B] so we draw an edge from T2->T1 giving us the following cycle.
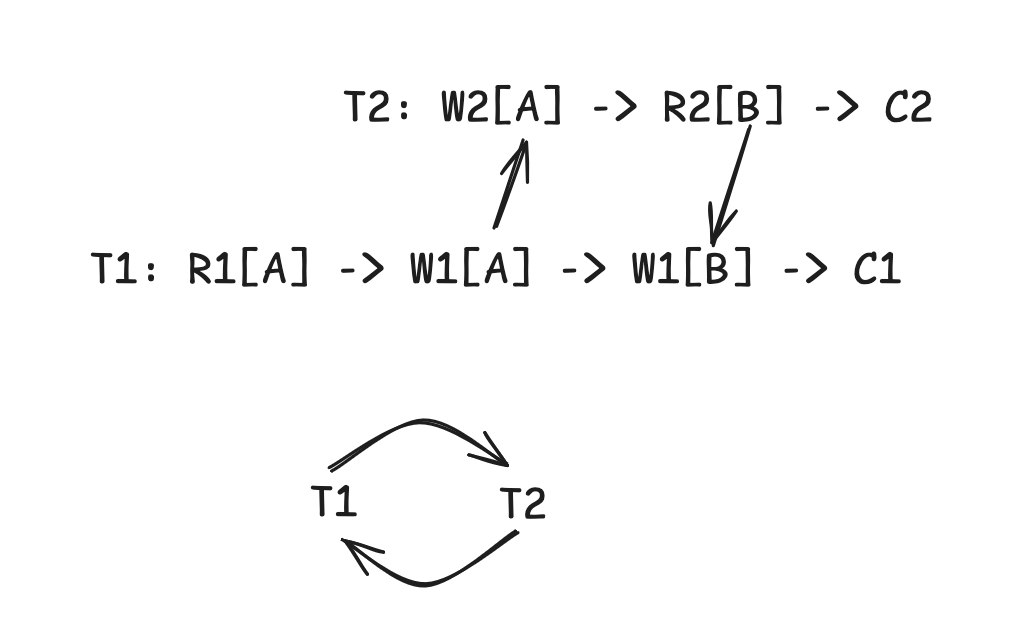
T1: BEGIN
T1: R(A)
T1: W(A)
T2: BEGIN
T2: W(A)
T2: R(B)
T1: W(B)
T1: COMMIT
T2: COMMIT
This is a problem because if the serial order was T1->T2 then W1[B] happens before R2[B], and the result of T2's program might be different if it had read that write. On the other hand, if the order was T2->T1, then W2[A] would precede R1[A], potentially changing T1's behavior when writing A.
Reading this book has been super helpful, and I’m looking forward to digging into the rest of it to see how these ideas continue to build on top of each other.